What is the intersection point for equations x-3=0 and y-5=0?

a) 5,3
b) 3,5
c) 0,-5
d) None of these

Question by Mohit

---

According to the question,

x-3=0 and y-5=0
But, we know that we need two variables for forming a line on the graph. But here we got only x as the variable in first equation and y as the variable in the second equation. But here y is formed as 0y in first equation and x is formed as 0x in the second equation. But in the question they are shown as they are not present.
Now they equations became,
x+0y-3=0 and 0x+y-5=0
Now if we take x=3 and y=0;
$\Rightarrow$ 3+0-3=0
$\Rightarrow$ 0=0
$\therefore$ x=3 and y=0 satisfy the equation.

Now if we take x=3 and y=5;
$\Rightarrow$ 3+(0)(5)-3=0
$\Rightarrow$ 3+0-3=0
$\Rightarrow$ 3-3=0
$\Rightarrow$ 0=0
$\therefore$ x=3 and y=5 satisfy the equation.

Now for the equation 0x+y-5=0,
Now if we take x=0 and y=5,
$\Rightarrow$ 0+5-5=0
$\Rightarrow$ 0=0
$\therefore$ x=0 and y=5 satisfy this equation

Now if we take x=3 and y=5,
$\Rightarrow$ (0)(3)+5-5=0
$\Rightarrow$ 0+5-5=0
$\Rightarrow$ 0=0
$\therefore$ x=3 and y=5 satisfy the equation.

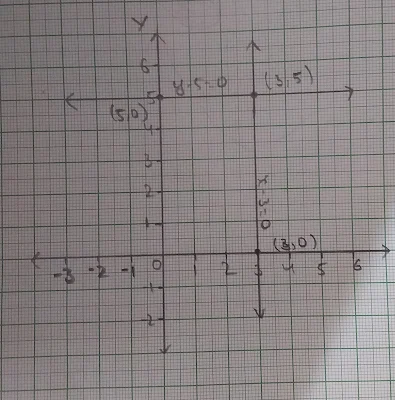
The both equations have point (3,5) as common so they would intersect at (3,5).
So, option B is correct.

The graph will look like this:

If you have any queries or you have doubt in any question you can contact us via email and describe your issue via email. We will try to publish your question with answer on our website, but those questions would only be published which are difficult and most students that get doubt in it. But, we will mail you the answer of your question.
Note: Any wrong question might lead to strict ban on you and we will take strict action on you.